GLISSETTE TANGENTIELLE
Tangential
Glissette, Tangentiale Gleitkurve
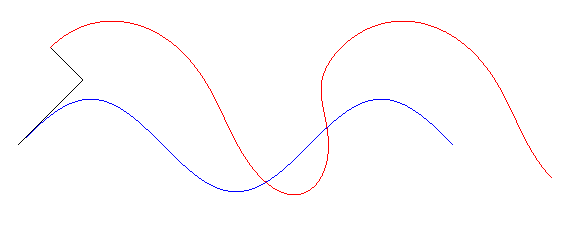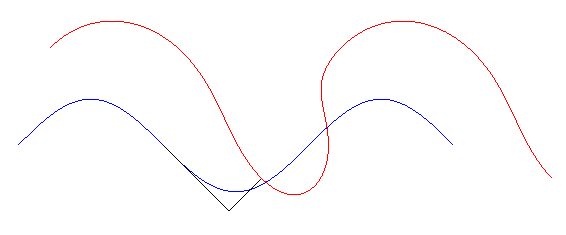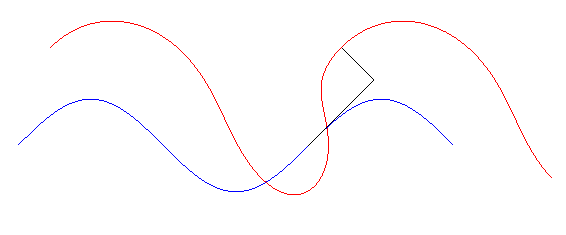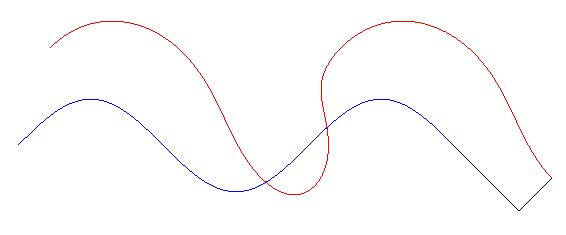
Glissette tangentielle d'une sinusoïde
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
GLISSETTE TANGENTIELLE
Tangential
Glissette, Tangentiale Gleitkurve

Glissette tangentielle d'une sinusoïde
| Nom maison.
Animations réalisées par Alain Esculier. |
| Paramétrisation cartésienne pour une glissette
de coordonnées X,Y dans le repère de Frenet, la courbe
de départ étant paramétrée par |
Les glissettes tangentielles d'une courbe (C) sont les traces dans le plan fixe des points d'un plan lié à une tangente glissant sur la courbe (C) ; voir à glissette (cas n°1 dual). Autrement dit ce sont les trajectoires des points ayant des coordonnées fixes dans le repère de Frenet se déplaçant le long de la courbe.
La normale à la courbe roulant sans glisser sur la développée, les glissettes tangentielles sont les roulettes du mouvement plan sur plan de base la développée et de roulante la normale.
Lorsque le point traceur est sur la tangente, les glissettes sont les courbes équitangentielles associée à (C), et lorsqu'il est sur la normale, les glissettes ne sont autres que les courbes parallèle à (C).
CAS PARTICULIER DES COURBES ÉQUITANGENTIELLES (Y
=
0,
X = d)
| Paramétrisation cartésienne : |
Exemple de l'ellipse :
| Paramétrisation cartésienne : Notons que d'après le théorème de Holditch, l'aire balayée par le segment tangent vaut |
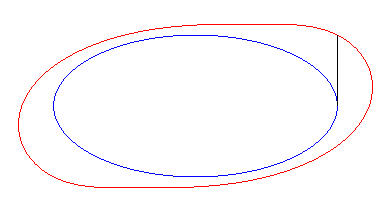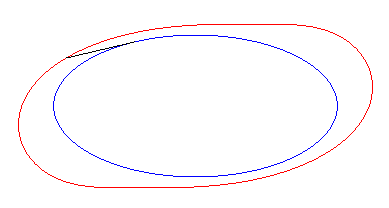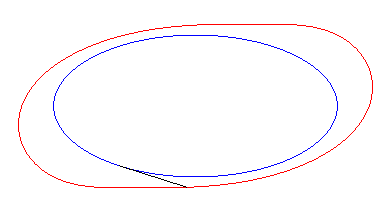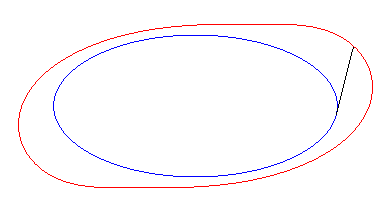 |
| La courbe de départ est une tractoire
de ses courbes équitangentielles.
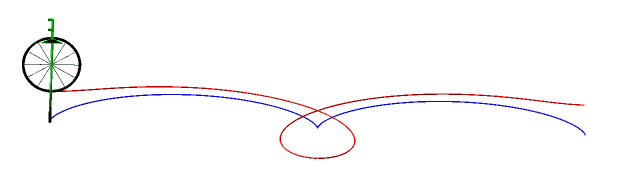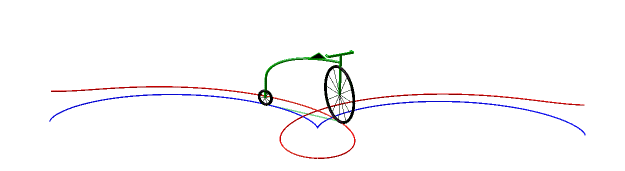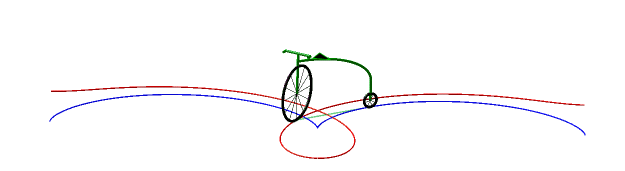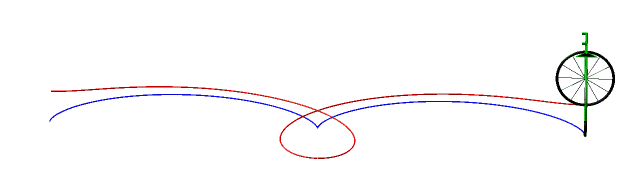
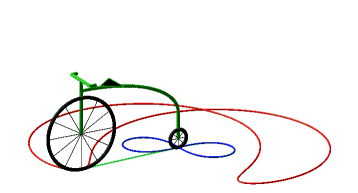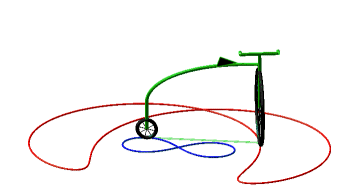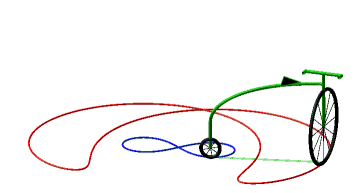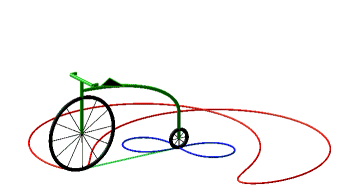
Donc, plus concrètement, les courbes équitangentielles sont les courbes des roues avant de vélos dont on impose à la roue arrière de suivre la courbe de départ. |
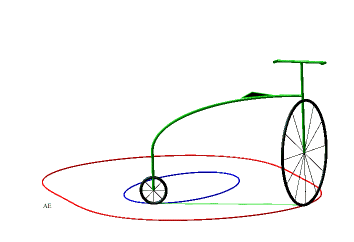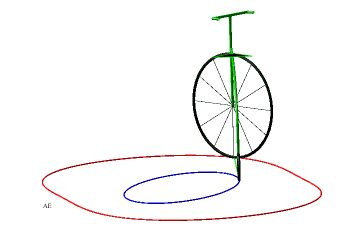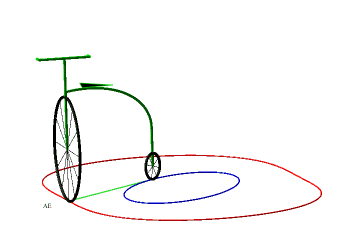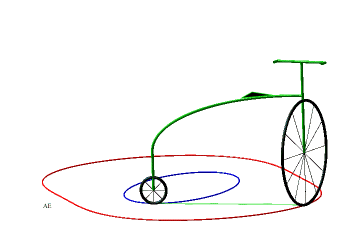 |
Ci-dessous, cas de la cycloïde
et de la lemniscate de Bernoulli.
 |
 |
Voir les syntractrices,
équitangentielles de la tractrice.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2019